The NIOSH Lifting Equation is an ergonomic assessment tool that calculates a recommended weight limit (RWL) for a two-handed lifting or lowering task, and a lifting index (LI) that shows how risky the actual load is. Developed by the National Institute for Occupational Safety and Health and revised in 1991, it multiplies a 51 lb load constant by six multipliers for the hand position, travel distance, twisting, frequency and grip.
This guide explains the NIOSH Lifting Equation formula and each multiplier, shows how to measure the task variables, and walks through two worked examples. Want to skip the math? Our free NIOSH Lifting Equation calculator works out the recommended weight limit, lifting index and every multiplier as you enter the task.
Note: This is a lengthy post! If you’d rather work your way through this guide with a PDF file, click here to download step-by-step guides to all of our recommended ergonomic assessment tools.
What is the NIOSH Lifting Equation?
The Revised NIOSH Lifting Equation is a tool used by occupational health and safety professionals to assess the manual material handling risks associated with lifting and lowering tasks in the workplace.
A lifting task is defined as the act of manually grasping an object with two hands, and vertically moving the object without mechanical assistance. The NIOSH Lifting Equation considers several job task variables to determine safe lifting practices and guidelines.
The NIOSH Lifting Equation is widely accepted as valid in the field of occupational ergonomics, providing occupational health and safety professionals an objective ergonomic risk assessment tool for manual material handling tasks. The NIOSH Lifting Equation is a great way to identify ergonomic opportunities and prioritize ergonomic improvement efforts, and it also provides an objective baseline from which you can document ergonomic improvements.
Recommended weight limit (RWL) and lifting index (LI)
Recommended Weight Limit (RWL): Answers the question… “Is this weight too heavy for the task?”
The primary product of the NIOSH equation is the Recommended Weight Limit (RWL), which defines the maximum acceptable weight (load) that nearly all healthy employees could lift over the course of an 8-hour shift without increasing the risk of musculoskeletal disorders (MSD) to the lower back.
Lifting Index (LI): Answers the question… “How significant is the risk?”
In addition, a Lifting Index (LI) is calculated to provide a relative estimate of the level of physical stress and MSD risk associated with the manual lifting tasks evaluated. A Lifting Index value of 1.0 or less indicates a nominal risk to healthy employees. A Lifting Index greater than 1.0 denotes that the task is high risk for some fraction of the population. As the LI increases, the level of injury risk increases correspondingly. Therefore, the goal is to design all lifting jobs to accomplish an LI of 1.0 or less.
| Lifting index | Risk | What to do |
|---|---|---|
| 1.0 or less | Nominal risk for most healthy workers | Keep the task design |
| More than 1.0, up to 3.0 | Increased risk for some workers | Redesign the task to bring the LI to 1.0 or lower |
| More than 3.0 | High risk for many workers | Redesign the task |
Uses of RWL and LI: The RWL and LI can be used to guide or engineer lifting task design in the following ways:
- Individual multipliers that determine the RWL can be used to identify specific weaknesses in the design.
- The LI can be used to estimate the relative physical stress and injury risk for a task or job. The higher the LI value, the smaller the percentage of workers capable of safely performing these lifting job demands. So using the LI, injury risk of two or more job designs could be compared.
- The LI can also be used to prioritize ergonomic redesign efforts. For example jobs can be ranked by LI and a control strategy can be implemented based on a priority order of the jobs or individual lifting tasks.
NIOSH Lifting Equation formula
RWL = LC × HM × VM × DM × AM × FM × CM
LI = Load weight ÷ RWL
The NIOSH Lifting Equation always uses a load constant (LC) of 51 pounds, which represents the maximum recommended load weight to be lifted under ideal conditions. From that starting point, the equation uses several task variables expressed as coefficients or multipliers (In the equation, M = multiplier) that serve to decrease the load constant and calculate the RWL for that lifting task.
Each multiplier is 1.0 under ideal conditions and gets smaller as the task moves away from them. In US units:
| Multiplier | Task variable | Formula |
|---|---|---|
| HM (horizontal) | H: horizontal distance of the hands from the midpoint between the ankles, in inches | 10 ÷ H (1.0 if H is 10 in or less, 0 if more than 25 in) |
| VM (vertical) | V: height of the hands above the floor, in inches | 1 − 0.0075 × |V − 30| (0 if V is more than 70 in) |
| DM (distance) | D: vertical travel distance, in inches | 0.82 + 1.8 ÷ D (1.0 if D is 10 in or less, 0 if more than 70 in) |
| AM (asymmetric) | A: twisting angle, in degrees | 1 − 0.0032 × A (0 if A is more than 135 degrees) |
| FM (frequency) | F: lifts per minute, with the duration and V | From the NIOSH frequency table |
| CM (coupling) | C: grip quality, with V | 1.00 for good, 0.95 to 1.00 for fair (depending on V), 0.90 for poor |
Task variables needed to calculate the RWL:
- H = Horizontal location of the object relative to the body
- V = Vertical location of the object relative to the floor
- D = Distance the object is moved vertically
- A = Asymmetry angle or twisting requirement
- F = Frequency and duration of lifting activity
- C = Coupling or quality of the workers grip on the object
Additional task variables needed to calculate LI:
- Average weight of the objects lifted
- Maximum weight of the objects lifted
Frequency-independent RWL and LI
The Frequency-Independent Recommended Weight Limit (FIRWL) and the Frequency-Independent Lifting Index (FILI) are additional outputs of the NIOSH lifting calculator.
The FIRWL is calculated by using a frequency multiplier (FI) of 1.0 along with the other task variable multipliers. This effectively removes frequency as a variable, reflecting a weight limit for a single repetition of that task and allows equal comparison to other single repetition tasks.
The Frequency-Independent Lifting Index (FILI) is calculated by dividing the weight lifted by the FIRWL. The FILI can help identify problems with infrequent lifting tasks if it exceeds the value of 1.0.
NIOSH Lifting Equation calculator and software
The NIOSH Lifting Equation can be calculated by hand, but it’s much easier and a big time saver to use a calculator:
- Free NIOSH Lifting Equation calculator: enter the load, frequency, duration, coupling and hand positions and see the RWL, lifting index and every multiplier at the origin and destination as you type. Print the result or save it as a PDF.
- ErgoPlus Industrial: the NIOSH Lifting Equation calculator in our ergonomics software saves every assessment, so you can compare jobs, share reports and track improvements across worksites.
How to use the NIOSH Lifting Equation
Measure and record the task variables
The first step is to gather the needed information and measurements for lifting task variables.
Task variable data needed:
H = Horizontal Location of the object relative to the body
V = Vertical Location of the object relative to the floor
D = Distance the object is moved vertically
A = Asymmetry Angle or twisting requirement
F = Frequency and Duration of lifting activity
C = Coupling or quality of the workers grip on the object
L = Average & maximum Load or weight of the object
You can use a paper worksheet to assist you with data collection as pictured above (download the NIOSH data collection worksheet), or you may prefer to enter data directly into the calculator as variables are determined.
The following task variables are evaluated to calculate the multipliers that are used in the NIOSH equation to determine the RWL. Here are some quick explanations and guidelines that you can use to gather the needed measurements:
Horizontal Location of the Hands (H) – Measure and record the horizontal location of the hands at both the start (origin) and end (destination) of the lifting task. Measure and record the horizontal location of the hands at the end (destination) of the lifting task only if significant control is required. The horizontal location is determined by measuring the distance between the point projected on the floor directly below the mid-point of the hands grasping the object (load center), and the mid-point of a line between the inside ankle bones as pictured below:
Vertical Location of the Hands (V) – Measure and record the vertical location of the hands above the floor at the start (origin) and end (destination) of the lifting task. The vertical location is measured from the floor (or standing surface) to the vertical mid-point between the hand grasps as defined by large middle knuckle (3rd MCP joint) of the hand.
Vertical Travel Distance (D) – The vertical travel distance of a lift is determined by subtracting the vertical location (V) at the start of the lift from the vertical location (V) at the end of the lift. For a lowering task, subtract the V location at the end from the V location at the start. If you’re using ErgoPlus Industrial, there’s no need to worry about this one, the calculator will do this work for you.
Asymmetric Angle (A) – Measure the degree to which the body is required to twist or turn during the lifting task. The asymmetric angle is the amount (in degrees) of trunk and shoulder rotation required by the lifting task. Note: Sometimes the twisting is not caused by the physical aspects of the job design, but rather by the employee using poor body mechanics. If this is the case, no twisting (0 degrees) is required by the job. If twisting is required by the design of the job, determine the number of degrees the back and body trunk must twist or rotate to accomplish the lift. (i.e. 90° as pictured below)
Coupling (C) – Determine the classification of the quality of the coupling between the worker’s hands and the object as good, fair, or poor (1, 2, or 3). A good coupling will reduce the maximum grasp forces required and increase the acceptable weight for lifting, while a poor coupling will generally require higher maximum grasp forces and decrease the acceptable weight for lifting.
- 1 = Good – Optimal design containers with handles of optimal design, or irregular objects where the hand can be easily wrapped around the object.
- 2 = Fair – Optimal design containers with handles of less than optimal design, optimal design containers with no handles or cut-outs, or irregular objects where the hand can be flexed about 90°.
- 3 = Poor – Less than optimal design container with no handles or cut-outs, or irregular objects that are hard to handle and/or bulky (e.g. bags that sag in the middle).
Frequency (F) – Determine the average number of lifts per minute of the lifting task being evaluated, this is the lifting frequency. This information can often be verified by asking for average production rates from a group leader, supervisor, or production manager. You can also accomplish this by determining the number of lifts per minute during a short sampling period. NIOSH recommends a 15-minute sampling or observation period. The Frequency (F) value will be between 0.2 lifts/minute and 15 lifts/minute. For lifting tasks with a frequency less than .2 lifts per minute (>1 lift every 5 minutes), you will use the minimum frequency of .2 lifts/minute.
Load (L) – Determine the weight of the object lifted. If necessary, use a scale to determine the exact weight. If the weight of the load varies from lift to lift, you should record the average and maximum weights lifted.
Duration (Dur) – Determine the lifting duration as classified into one of three categories: Enter 1 for short-duration, 2 for moderate-duration and 8 for long-duration as follows:
- 1 = Short – lifting ≤ 1 hour with recovery time ≥ 1.2 X work time
- 2 = Moderate – lifting between 1 and 2 hours with recovery time ≥ 0.3 X lifting time
- 8 = Long – lifting between 2 and 8 hours with standard industrial rest allowances
After task variables are determined, enter data into the calculator to determine the RWL and LI.
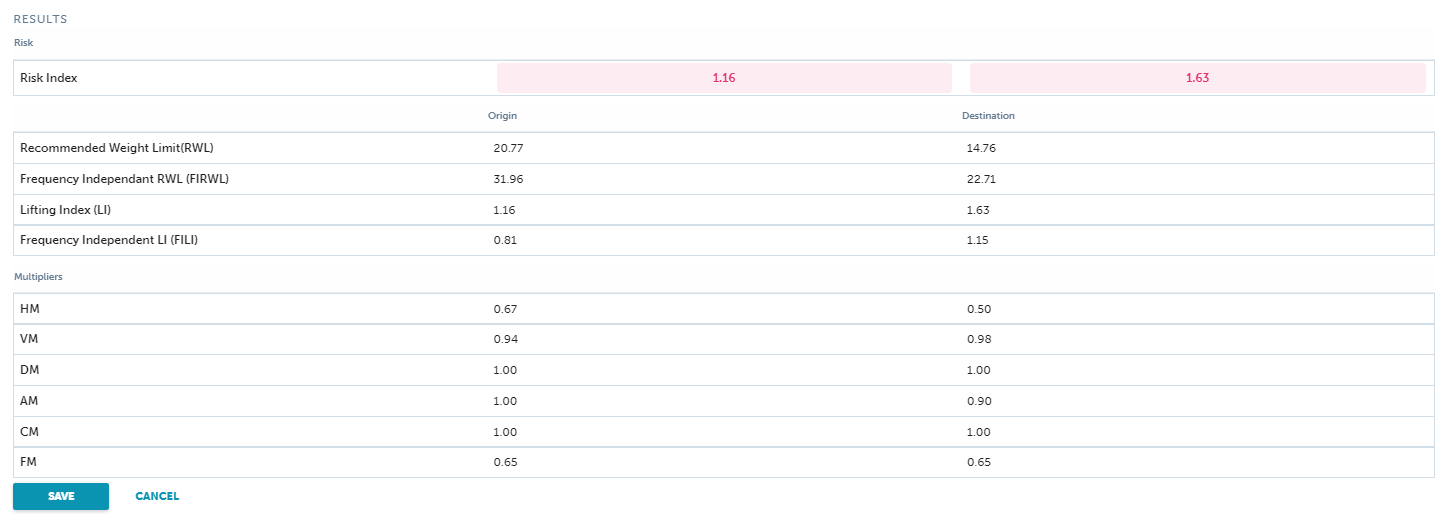
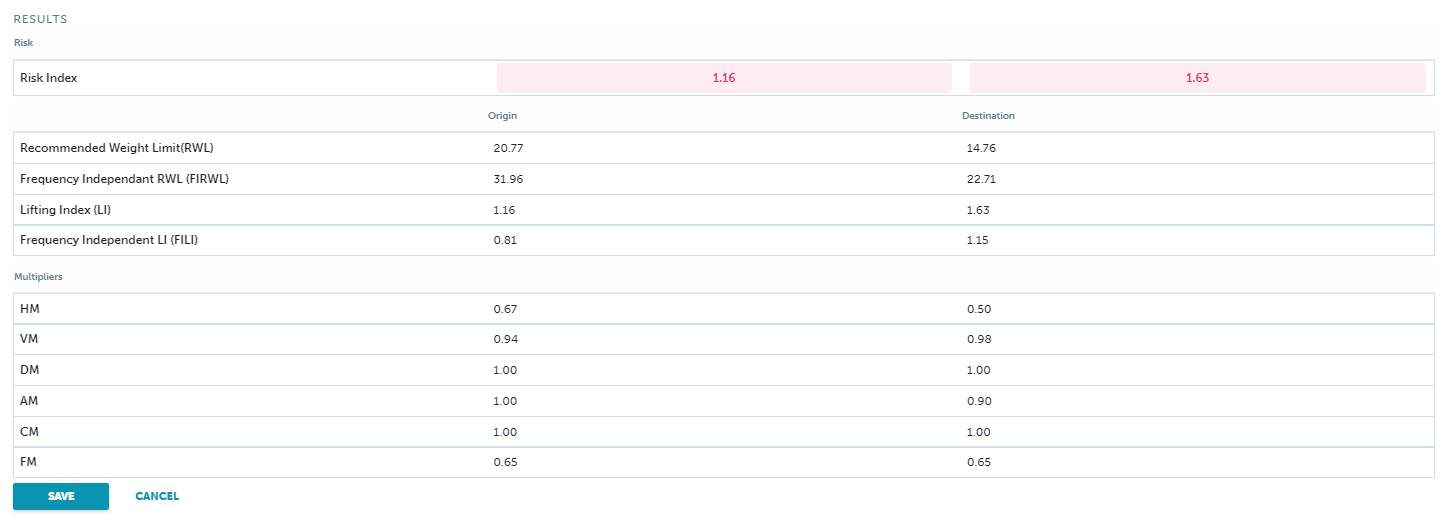
NIOSH Lifting Equation example 1: warehouse pick (lifting)
Step 1: Determine the task variables needed
The worker lifts and transfers containers from the rack pallet (Origin) to the picking cart (Destination), stepping toward the cart and pivoting his feet to perform this task. Significant control of the object is not required at the destination, therefore the only task variable needed at the destination is the vertical location of hands (V) which is needed to determine the Travel Distance (D).
Step 2: Determine and record the task variables
The Horizontal Location (H) of the hands is 15” at the origin. The Vertical Location (V) of the hands is 12-30”at the origin, but we will use the lowest level to assess the worst case. The Vertical Location (V) is 42” at the destination, therefore the Travel Distance (D) is 30”. The Asymmetric Angle (A) is 30 degrees at the origin. The container is of optimal design with handholds; therefore, coupling is defined as “good”. The average frequency of lifting in this manner is 1 lift every 2 minutes (.5 lifts per minute) over a duration of an 8-hour period.
Example 1 summary of task variable data:
H = 15” at the origin
V = 12” at the origin and 42” at the destination
D = 30” (calculated for you)
A = 30° at the origin
C = 1 (good – container is of optimal design with handhold cutouts)
F = .5 lifts/minute (1 lift every 2 minutes)
L = 28 lb. average load and 28 lb. maximum load
Dur = Long (lifting between 2 and 8 hours with standard industrial rest allowances for lunch and rest breaks)
Step 3: Use the calculator to find the RWL and LI
| Result | Origin |
|---|---|
| Horizontal multiplier (HM) | 0.67 |
| Vertical multiplier (VM) | 0.86 |
| Distance multiplier (DM) | 0.88 |
| Asymmetric multiplier (AM) | 0.90 |
| Frequency multiplier (FM) | 0.81 |
| Coupling multiplier (CM) | 1.00 |
| Recommended weight limit (RWL) | 18.95 lb |
| Lifting index (LI = 28 ÷ 18.95) | 1.48 |
| Frequency-independent RWL | 23.40 lb |
| Frequency-independent LI | 1.20 |
A lifting index of 1.48 means increased risk for some workers. The smallest multipliers show where the task design costs the most: the horizontal distance (HM 0.67) and the low starting height (VM 0.86). Open example 1 in the free NIOSH calculator.
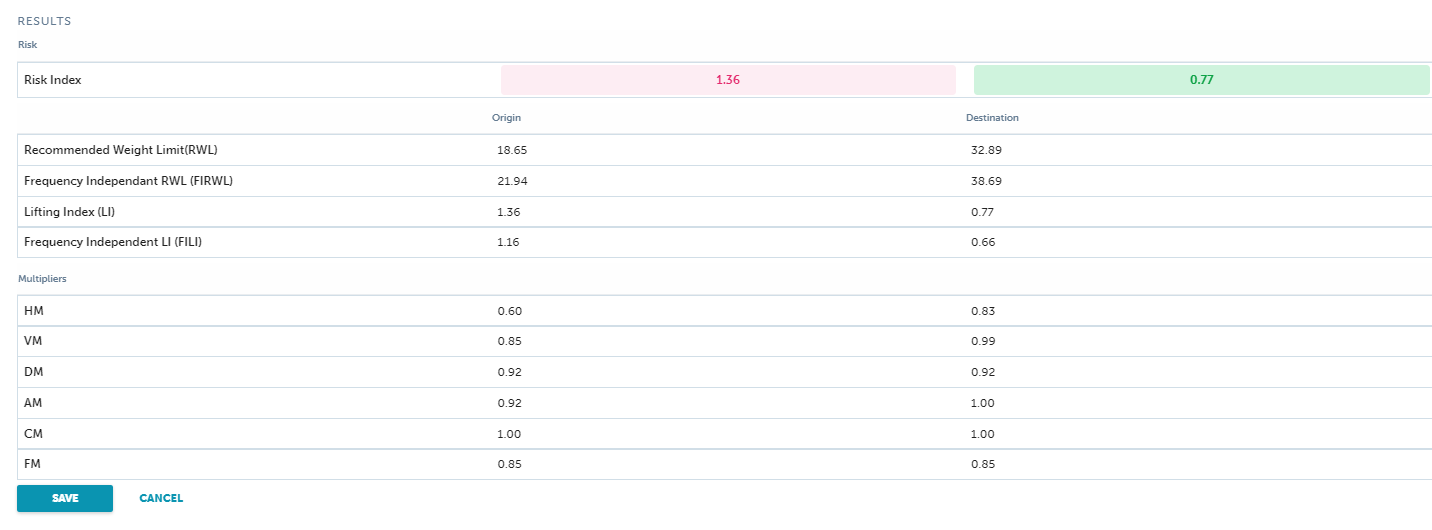
NIOSH Lifting Equation example 2: parts container (lowering)
Step 1: Determine the task variables needed
This assembly worker is required to lower a container of parts periodically throughout an 8-hour shift. The worker lowers the container from an upper incoming conveyor (Origin), stepping and pivoting to place the container on the workstation staging location (Destination). Significant control of the container is required at the destination to guide it to a precise staging location, so task variables will need to be determined at both the origin and destination.
Step 2: Determine and record the task variables
The Horizontal Location (H) is 16.75” at the origin, and 12” at the destination. The Vertical Location (V) is 49.5” at the origin, and 31” at the destination. The Travel Distance (D) is 18.5”. The Asymmetric Angle (A) is 25 degrees at the origin. Since pivoting the feet and stepping toward the destination is not restricted by job design and the container stays directly in front of the body (mid-sagittal plane), I would use 0 degrees for (A) at the destination.
(Note: Regarding (A) at the destination in this example: Remember that the lifting equation applications manual recommends that you assume that workers will not step and pivot. NIOSH acknowledges that this assumption may cause an overestimation of the Asymmetric multiplier’s reduction in the RWL but indicates that this assumption will provide the most conservative evaluation of the RWL. It’s obviously your call, but I prefer to stay away from such assumptions and try my best to evaluate the actual conditions of the lifting or lowering task.) The container is of optimal design with handholds (good), but the Coupling (C) is rated as fair because the high vertical hand position at the origin requires re-gripping. The average Frequency (F) of lowering this container is 1 lift every 12 minutes (< 0.2 lifts per minute) for 8 hours. Average and Max. Load (L) = 25.4 lbs.
Example 2 summary of task variable data:
H = 16.75 at the origin, 12” at destination
V = 49.5” at the origin and 31” at the destination
D = 18.5” (calculated for you)
A = 25° at the origin and 0° at the destination
C = 2 (fair -high vertical hand position at the origin requires re-gripping)
F = <.2 lifts/minute (1 lift every 12 minutes)
L = 25.4 lb. average load and 25.4 lb. maximum load
Dur = Long (lifting between 2 and 8 hours with standard industrial rest allowances for lunch and rest breaks)
Step 3: Use the calculator to find the RWL and LI
| Result | Origin | Destination |
|---|---|---|
| Horizontal multiplier (HM) | 0.60 | 0.83 |
| Vertical multiplier (VM) | 0.85 | 0.99 |
| Distance multiplier (DM) | 0.92 | 0.92 |
| Asymmetric multiplier (AM) | 0.92 | 1.00 |
| Frequency multiplier (FM) | 0.85 | 0.85 |
| Coupling multiplier (CM) | 1.00 | 1.00 |
| Recommended weight limit (RWL) | 18.65 lb | 32.89 lb |
| Lifting index (LI) | 1.36 | 0.77 |
| Frequency-independent RWL | 21.94 lb | 38.69 lb |
| Frequency-independent LI | 1.16 | 0.66 |
The lowering task is riskiest at the origin, where the hands start high and far from the body (VM 0.85, HM 0.60): a lifting index of 1.36 means increased risk for some workers. At the destination the lifting index is 0.77, nominal risk. Open example 2 in the free NIOSH calculator.
NIOSH Lifting Equation, Snook Tables or WISHA?
Each manual handling tool answers a slightly different question, so choose the one that matches the task:
| Tool | Use it for | Main output |
|---|---|---|
| NIOSH Lifting Equation | Two-handed lifting and lowering | Recommended weight limit and lifting index |
| Snook Tables | Lifting, lowering, pushing, pulling and carrying | Design goal weight or force, and a risk index |
| WISHA Lifting Calculator | Quick screening of a lift | Weight limit and lifting index |
| REBA or RULA | Awkward postures | A posture risk score |
FAQ
Common questions about the NIOSH Lifting Equation
What is the NIOSH Lifting Equation formula?
The recommended weight limit is RWL = LC × HM × VM × DM × AM × FM × CM, where LC is the 51 lb load constant and the six multipliers cover the horizontal and vertical hand position, the travel distance, the twisting angle, the lifting frequency and the grip. The lifting index is LI = load weight ÷ RWL.
Why is the load constant 51 pounds?
The 51 lb (23 kg) load constant is the most weight NIOSH recommends lifting under ideal conditions: the hands 10 inches from the body and 30 inches off the floor, a short lift of 10 inches or less, no twisting, infrequent lifting and a good grip. Each multiplier reduces it as the task moves away from those conditions.
How is the lifting index calculated?
Divide the weight of the load by the recommended weight limit. In example 1 of this guide, a 28 lb container with an RWL of 18.95 lb gives a lifting index of 1.48. A lifting index of 1.0 or less is the design goal.
Who developed the Revised NIOSH Lifting Equation?
NIOSH researchers Thomas Waters, Vern Putz-Anderson, Arun Garg and Lawrence Fine revised the original 1981 equation in 1991 and published it in Ergonomics in 1993. NIOSH followed it with the Applications Manual for the Revised NIOSH Lifting Equation in 1994.
Can the NIOSH Lifting Equation be used for jobs with several different lifts?
Yes. For jobs with several lifting tasks, the Applications Manual describes a composite lifting index (CLI) that combines the tasks, weighted by how often each one happens. This guide and the free calculator cover a single lifting task, which is the place to start: work out the RWL and LI for each task first.
Can I use the NIOSH Lifting Equation in metric units?
Yes. The metric version uses a 23 kg load constant and measures the hand positions and travel distance in centimeters. The free NIOSH Lifting Equation calculator switches between US and metric units for you.
When should I use the Snook Tables or the WISHA Lifting Calculator instead?
Use the Snook Tables for pushing, pulling and carrying, which the NIOSH equation does not cover. The WISHA Lifting Calculator is a quicker screening tool for lifts. For awkward postures rather than load weight, use REBA or RULA.
Is there a NIOSH Lifting Equation worksheet?
Yes. Download the NIOSH data collection worksheet (PDF) to record the task variables, then enter them in the free NIOSH Lifting Equation calculator.
References
- Waters, T. R., Putz-Anderson, V., Garg, A., & Fine, L. J. (1993). Revised NIOSH equation for the design and evaluation of manual lifting tasks. Ergonomics, 36(7), 749–776. https://doi.org/10.1080/00140139308967940
- Waters, T. R., Putz-Anderson, V., & Garg, A. (1994). Applications Manual for the Revised NIOSH Lifting Equation (DHHS (NIOSH) Publication No. 94-110). https://www.cdc.gov/niosh/docs/94-110/ (PDF copy)
Free Download: Step-by-Step Guides to Recommended Ergonomic Assessment Tools
Learn how to conduct fast and accurate assessments using the most popular ergonomic assessments tools.
Please fill out the form below and we’ll email a link to your resources right away. 